PID
Basic theory of PID control
Table of Content
Basics Concepts Before Learning PID
Proportional Controller "P" in PID Controller
Integrational Controller "I" in PID Controller
Derivative Controller "D" in PID Controller
Basics Concepts Before Learning PID
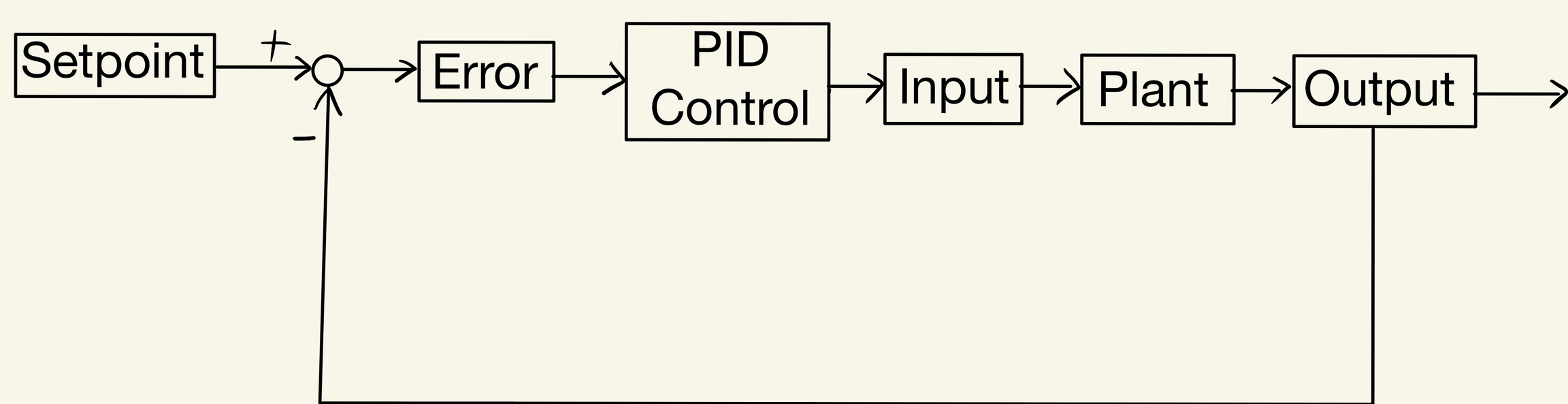
Before learning anything about PID, we first should define some keywords and some important terms for our future use.
First, we have a "Plant", which is the system we want to control.
Then we have "Input" and "Output". Our goal is to find out how we generate the input such that our system can produce the desired controlled variable, which is the output.
Other than that, we also have something called "Setpoint", which is the desired variable output that we want. Noted that the Output may not be exactly the same as the Setpoint or else we actually no need to do any controlling system to the Plant.
The difference between the Setpoint and the Output is called the "Error" or the "Error Term". If the output is exactly the same as the Setpoint, the Error will go to zero, which is our goal.
In PID, we will talk this Error term and convert it into a suitable acutated command, so that over time, the Error will drop to zero.
Proportional Controller "P" in PID Controller
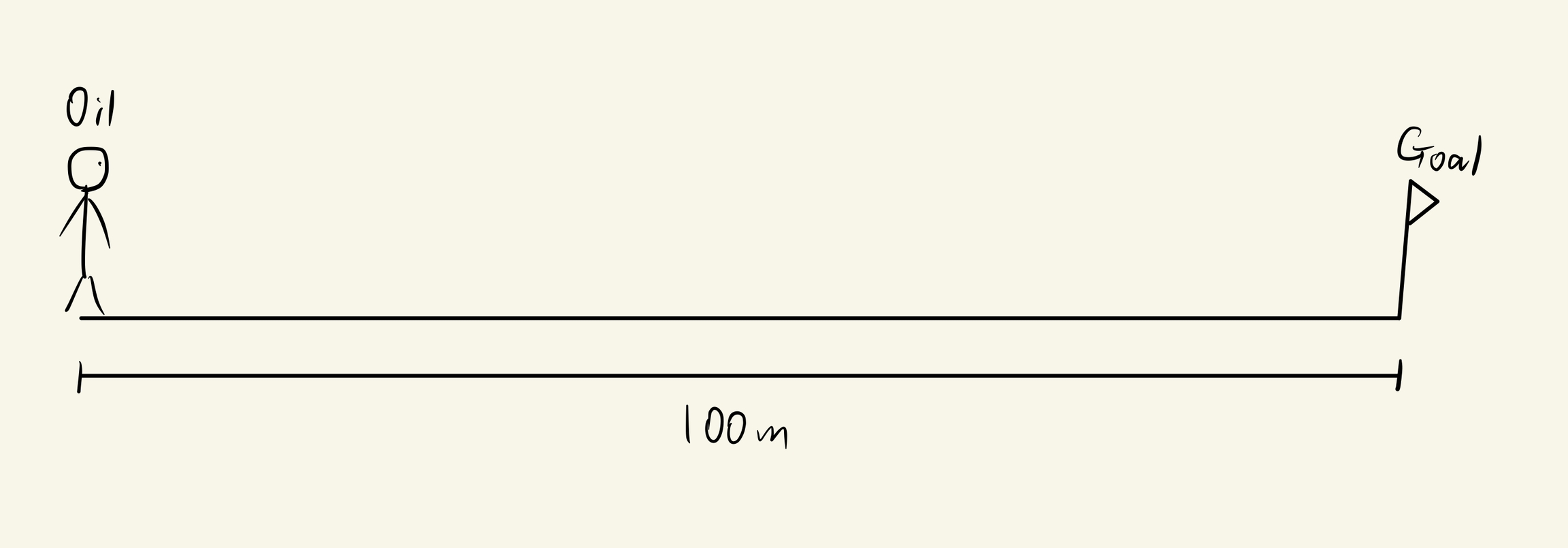
Now, imagine Oil is at the start point of a path. The goal is 100m away from Oil. What Oil is doing, is to move from the start point to the goal.
So for the current situation:
Setpoint = 100
Input = Oil's speed
Output = Distance between Oil and the start point of the path
Error = 100 - Output
Error at time 't = 0' = 100 - 0 = 100
Now, Oil's brain will do the PID control calculation such that the speed of Oil will be calculated and Oil will walk with the speed calculated.
One way Oil' 's brain can do, this is to use the current Error to decide the speed of Oil.
Here we will set our controller value to 0.1, which means the current speed of Oil would be Error x 0.1.
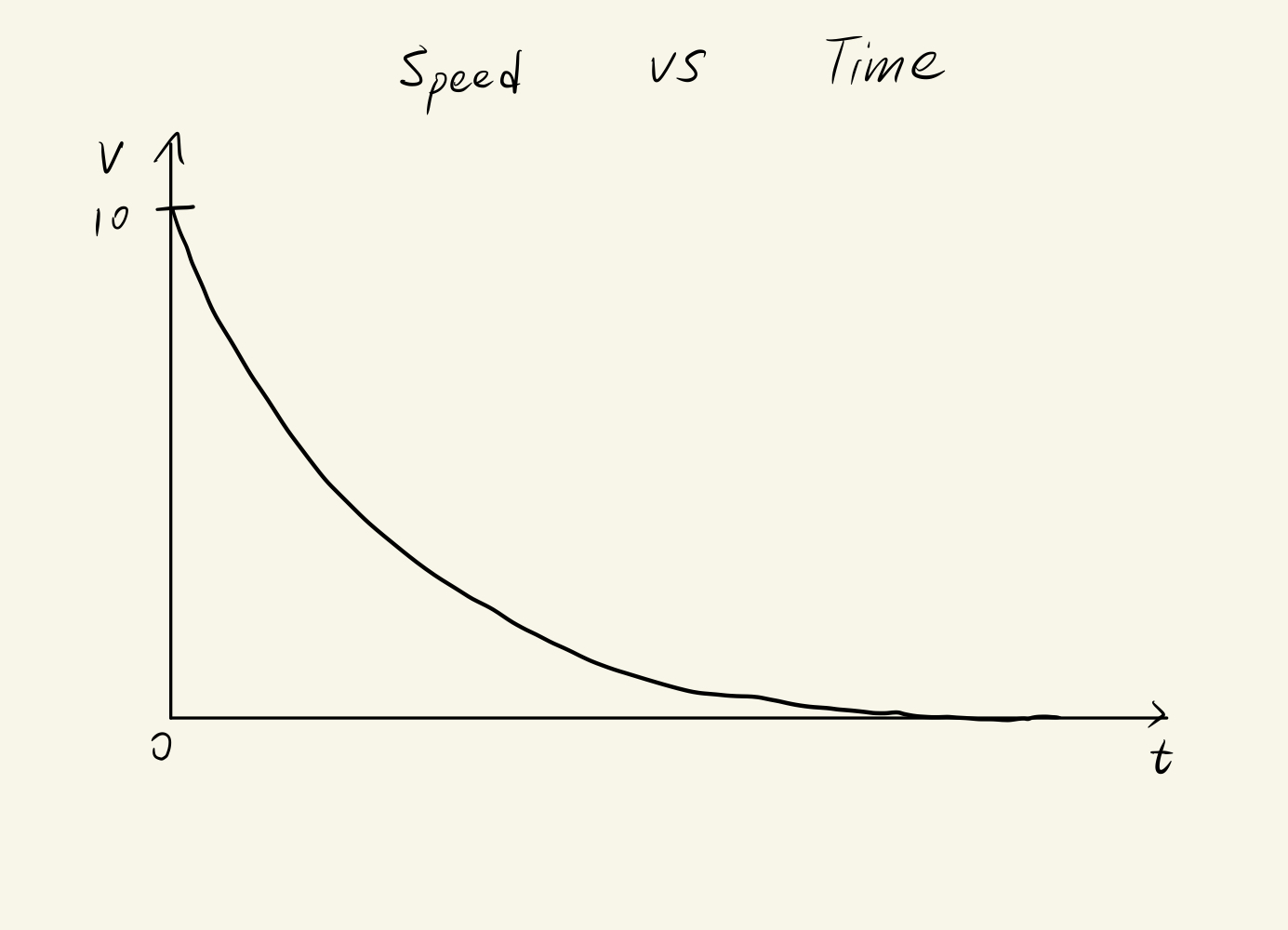
At time 't = 0', the Error of Oil would be 100. Therefore the speed of Oil at the beginning is 100 x 0.1 = 10m/s.
So after the first second, Oil is still 90m away from his goal.
The controller value we have just mentioned is called "kp". It is a constant which is used to control "P" in a PID controller.
Using this proportional controller, we start reducing the Error quickly since we are far away from our goal and gradually slow down as we get closer and closer to the goal. In this way, we would eventually and asymptotically reach the goal, at which time the Error would be zero. The proportional controller will multiply 0 by 0.1 which would generate a speed of zero for Oil, stopping at the goal.

If we want to adjust the amount of time Oil took to reach the goal, we could increase or decrease the kp.
No matter how large or how small the kp is, Oil can eventually get to the goal.
Formula: P=kp∗e(t)
kp: constant determined by yourself e(t): Error at time 't = t'.
Try It Yourself
Try to draw graphs of Distance versus Time and Speed versus time with different kp to see how they are different from the two above.
How to Determine the optimal value for kp?
Kp is a constant determined by the one who writes the program. If you have drawn yourself some graphs required in the "Try It Yourself" session, you may find out that, the higher the kp, the faster the output can "touch" the Setpoint. However, higher kp will lead to larger fluctuations after the output reaches the Setpoint. Therefore, it is up to you. If you want the Plant to reach the desired Setpoint in a shorter time, use a larger kp, else, use a lower kp.
Integrational Controller "I" in PID Controller
The Proportional Controller seems nice. No matter how large or how small the kp is, Oil can eventually get to the goal. But is this the best way to control the speed of Oil in every situation?
The answer is "No".
Imagine now, Doraemon has given a "Take-Copter" (A device which Oil can put on top of Oil's head such that Oil can hover) to Oil, and asks Oil to control the Take-Copter such that Oil can fly upward with a certain speed.
Doraemon set a goal of 100m high for Oil. After learning the Proportional Controller, Oil immediately applied it to the Take-Copter. However, something unexpected happened.
Oil first set the kp to 0.1. Before start hovering, the Error is 100. After multiplying the Error by the kp, the upward speed of Oil at the beginning would be 10m/s.
Remember what we have mentioned when we learnt Proportional Controller, no matter how large or how small the kp is, Oil can eventually get to the goal. However, when Oil reaches 100m above the ground, the Take-Copter will shut down as it does not need to provide any upward thrust for Oil to fly upward. Therefore, Oil drops.
After dropping for a while, the Take-Copter realise that Oil is not staying the at goal with a certain amount of Error instead of zero, so the Take-Copter will function again and let Oil fly again.
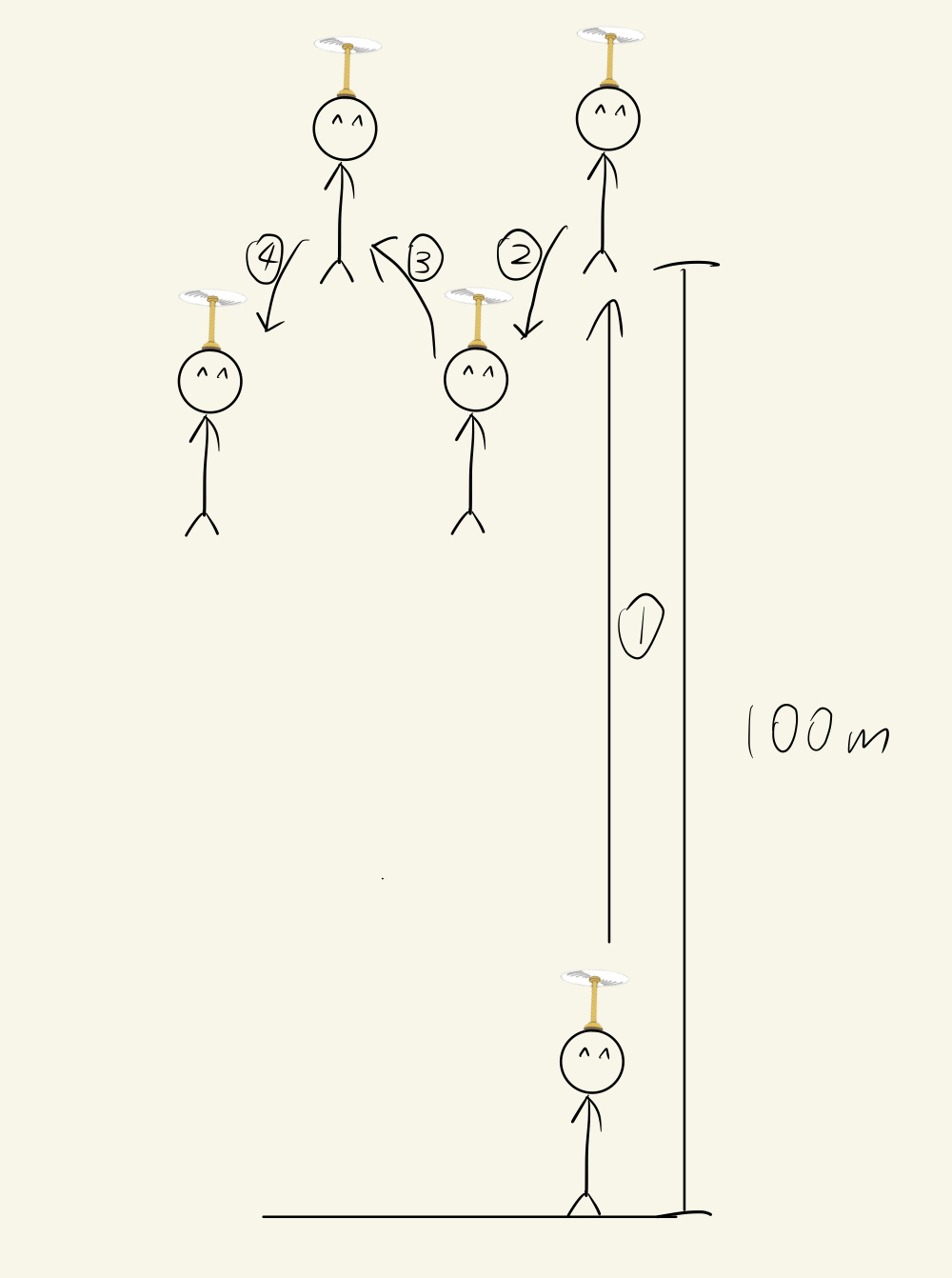
There is a certain propeller speed, where the upward thrust provided by the Take-Copter is exactly the same as the weight of Oil (although Oil is light as a feather). At that moment, Oil will no longer move upward and stay hovering below our target.
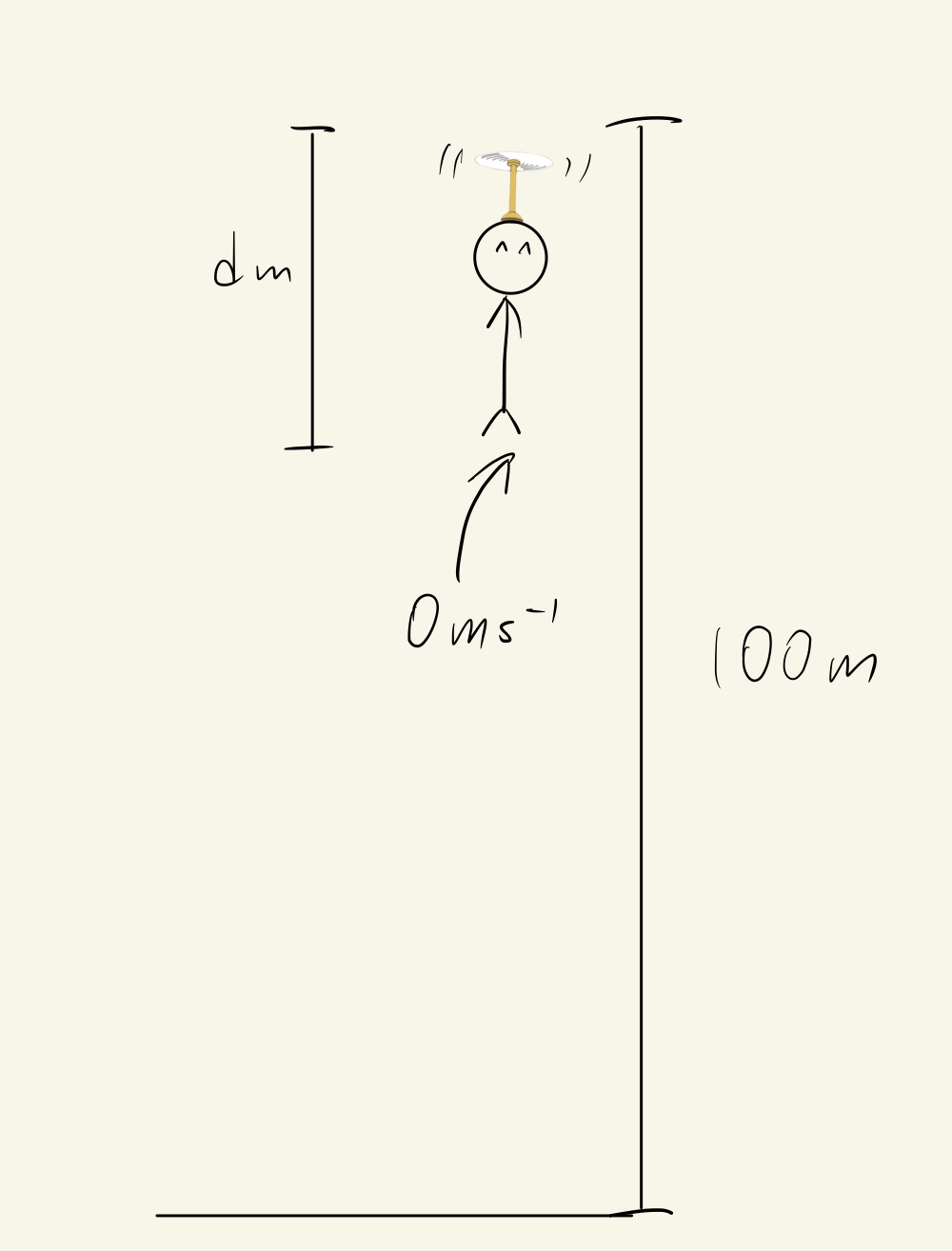
Take a closer look at the Take-Copter. Assume the Take-Copter need 100rmp to make Oil hover without moving upward or downward. If Oil sets the kp to 1, then Oil will hover at the ground as 100/1 = 100m below the goal, which means there will not be any upward net force for Oil.
If Oil sets the kp to 5, then Oil will hover at 100/5 = 20m below the goal.
Even if Oil sets the kp to 100, then Oil will still hover at 100/100 = 1m below the goal.
As you can see, Oil will never hover exactly at the goal which is 100m above the ground. The Error will never go to zero, it will just go smaller and smaller and it only "seems to be zero".
This indicates that the Proportional Controller does not work in any situation. It works for Oil's walking example, but not Oil's flying example which creates a constant Error.
The constant Error created in Oil's flying example is called the "Steady State Error".
How can we eliminate or deal with this Error?
We can use the Integrational Controller.
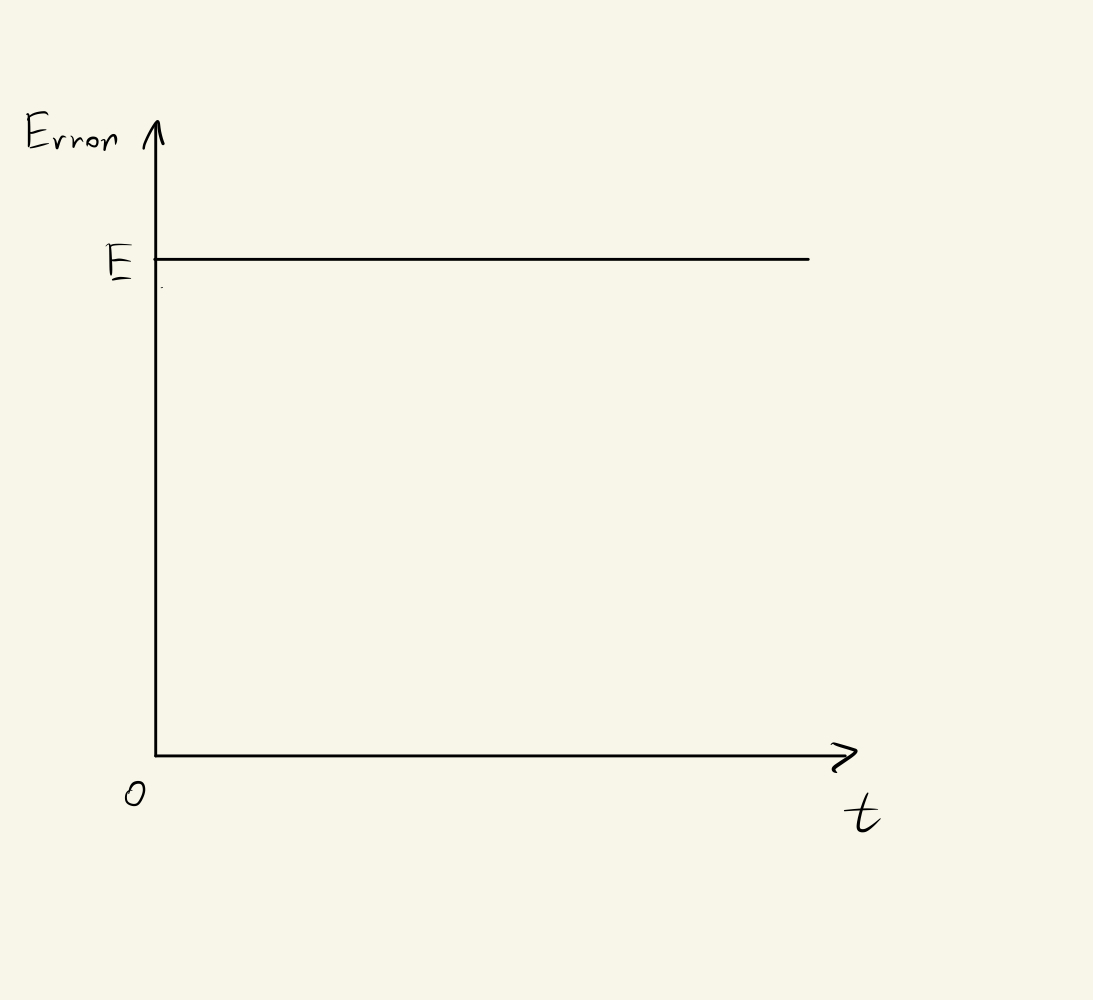
When Oil hovers below the goal, Oil is at a Steady State, and there will be a constant Error. What the Integrational Controller do, is to sum up (or we say "integrate") the Error. As long as there is an Error, the integrated value will keep changing.
Since we have a constant Error in the above situation, the increased value will increase the turning speed of the Take-Copter, making the oil rise up higher.
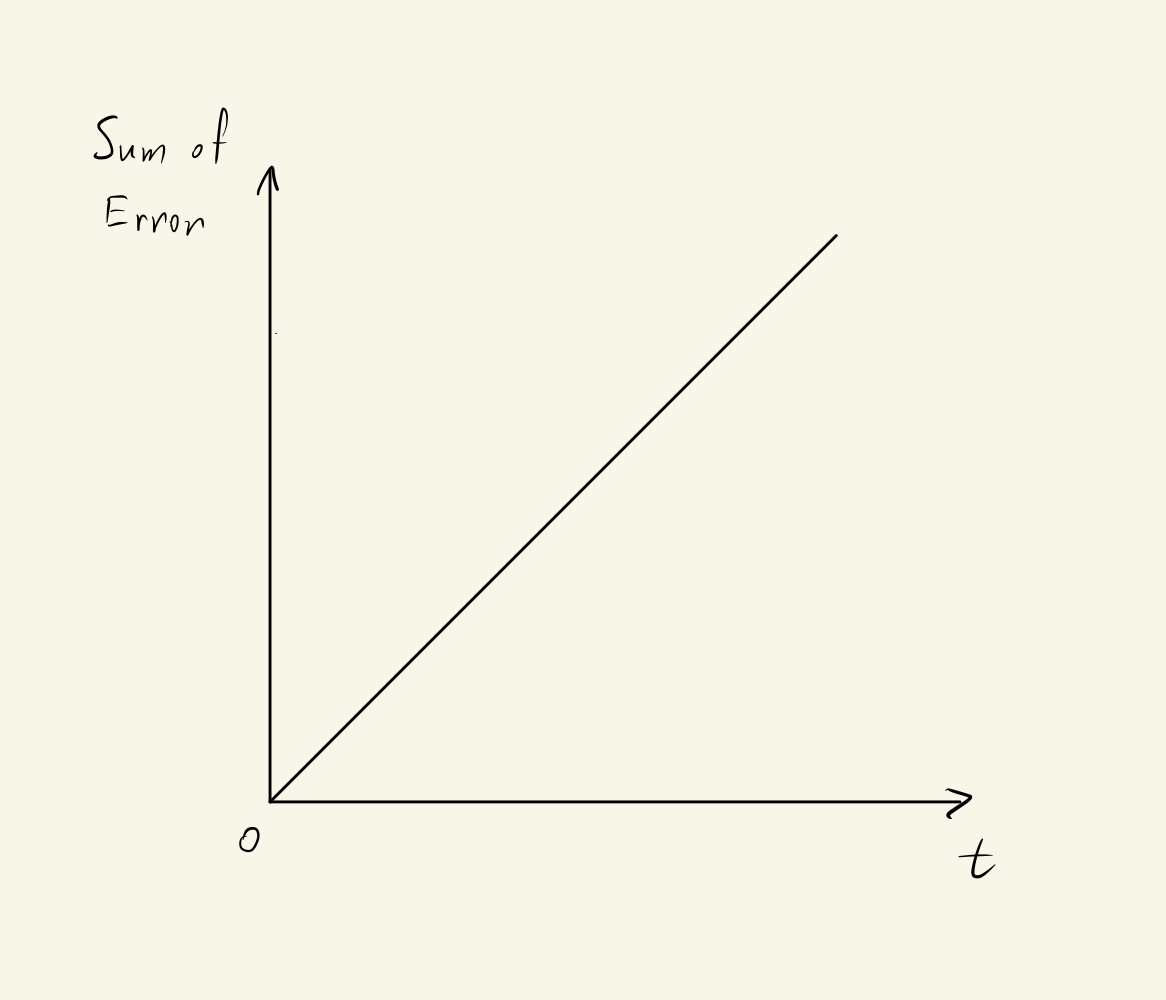
Cooperating with the Proportional Controller, the Integrational Controller can drive the Error down to zero. When Oil reaches 100m, the Proportional Controller does nothing since the Error is zero. But the Integrational Controller has been summing and subtracting values until the Take-Copter came to rest at 100rpm, which is required for Oil to hover, without rising and falling. At that moment, the output from the Integrational Controller would be zero, since the input to the controller at this point is zero.
To use the Intrgrational Controller, we have to define a constant "ki". It is used to multiply by the sum of Error.
By integrating the Error of the Plant from it is turned on, to the present, we would get a very large value of the sum of the Error. Therefore, the "ki" is always extremely small and we may need to set a limit for the sum.
Formula: I=ki∗∫0t e(t)dx ki: constant determined by yourself
How to Determine the optimal value for ki?
Actually, we seldom use ki. Some situations such as drones or motors connecting some load may require an integral controller, but in most cases, we do not need an integral controller. But when you really face these kinds of situations, we usually start with an extremely small ki such as 0.00001, since the sum of the Error will gain larger and larger in the long run, a smaller ki will prevent the output from being too uncontrollable.
Derivative Controller "D" in PID Controller
By just using "P" and "I", is this the best way to control our Plant?
The answer is still "No".
Imagine, using the Oil using Take-Copter scenario, when Oil uses a very large kp such that he can rise very fast and reach 100m in a very short time. However, because of the large kp, the rasing of Oil will overshoot, which means Oil will rise above 100m for a certain time before falling back to 100m. With the aid of the Integrational Controller, Oil may rise even higher before Oil can become steady and hover. However, when Oil rises higher than 100m, the Error calculated would be negative (e.g. Oil is at 110m now. Error = Setpoint - Output = 100 - 110 = -10m). The Take-Copter will then provide a downward thrust for Oil to fall at a faster speed such that Oil can reach 100m. Again, because of the very large kp, the Take-Copter would overshoot again and Oil would fall below 100m.
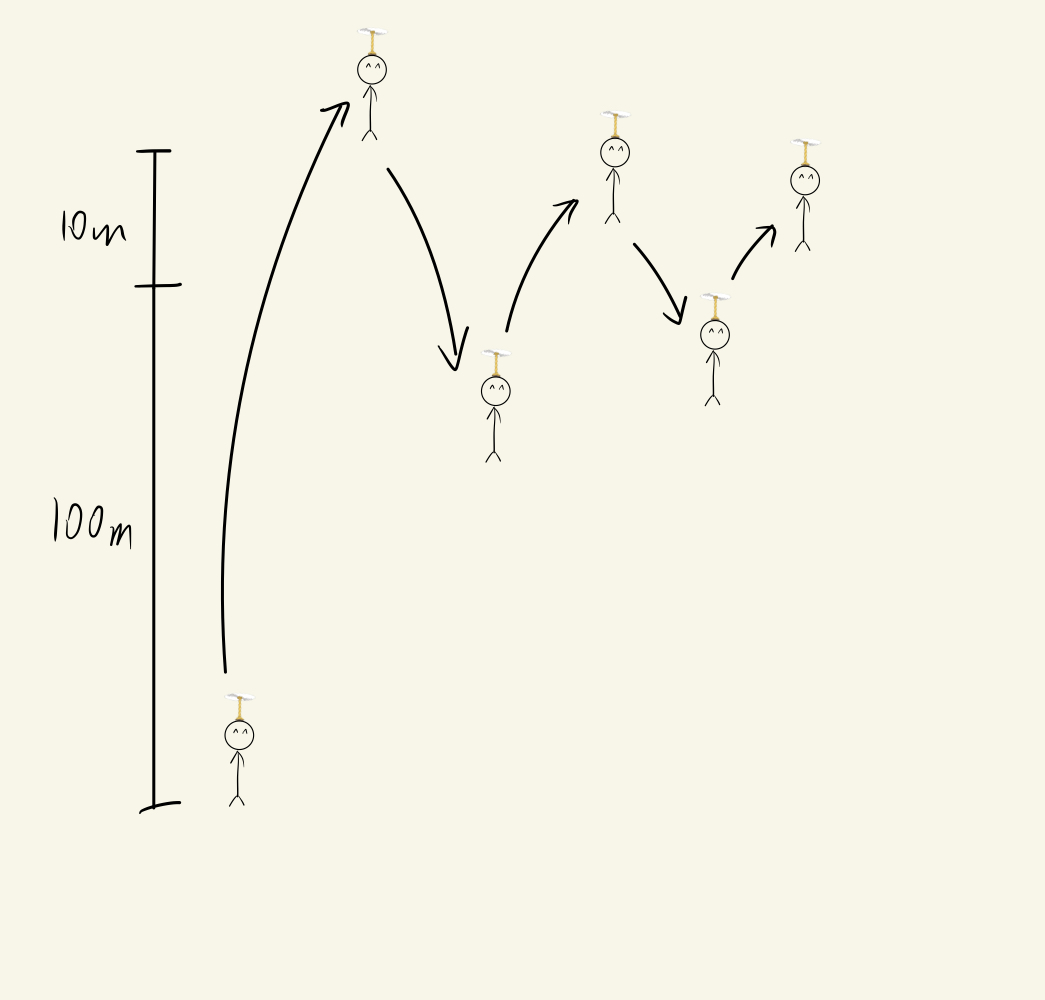
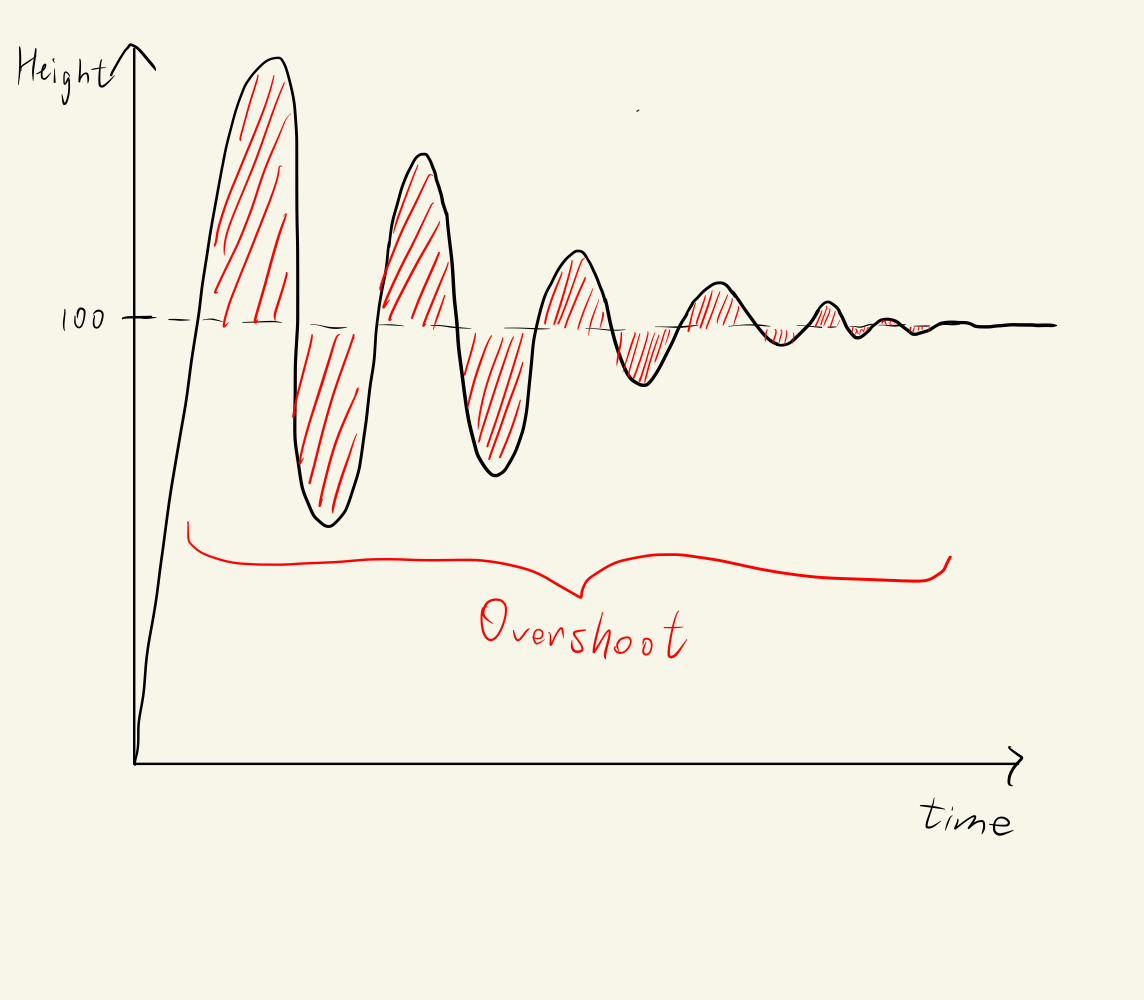
Overshooting is of course what we do not want. It increases the time required for the Plant to stay at our Setpoint steadily. How can we reduce overshooting and the time required for the Output of the Plant to stop right at our Setpoint? We will need the Derivative Controller "D".
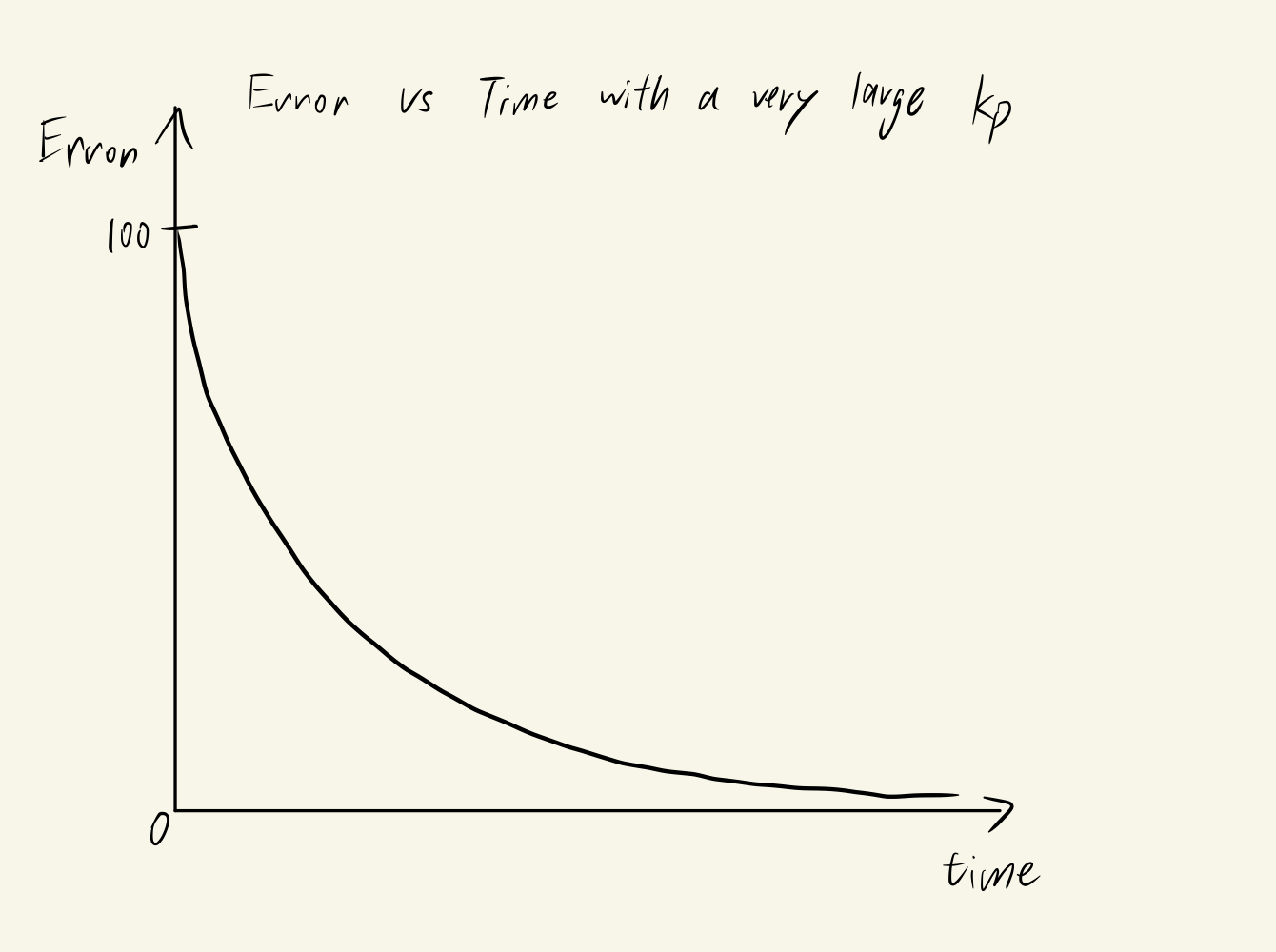
The Derivative Controller can produce the rate of change of the Error, which is how fast the Error is decreasing or increasing. For example, if Oil uses a very large kp for his Take-Copter (let's say, kp = 100), Oil will rise very fast at the beginning, which means the Error is quickly decreasing. The rate of change of Error would be very high in magnitude but negative, which would produce a negative value for the Derivative path.
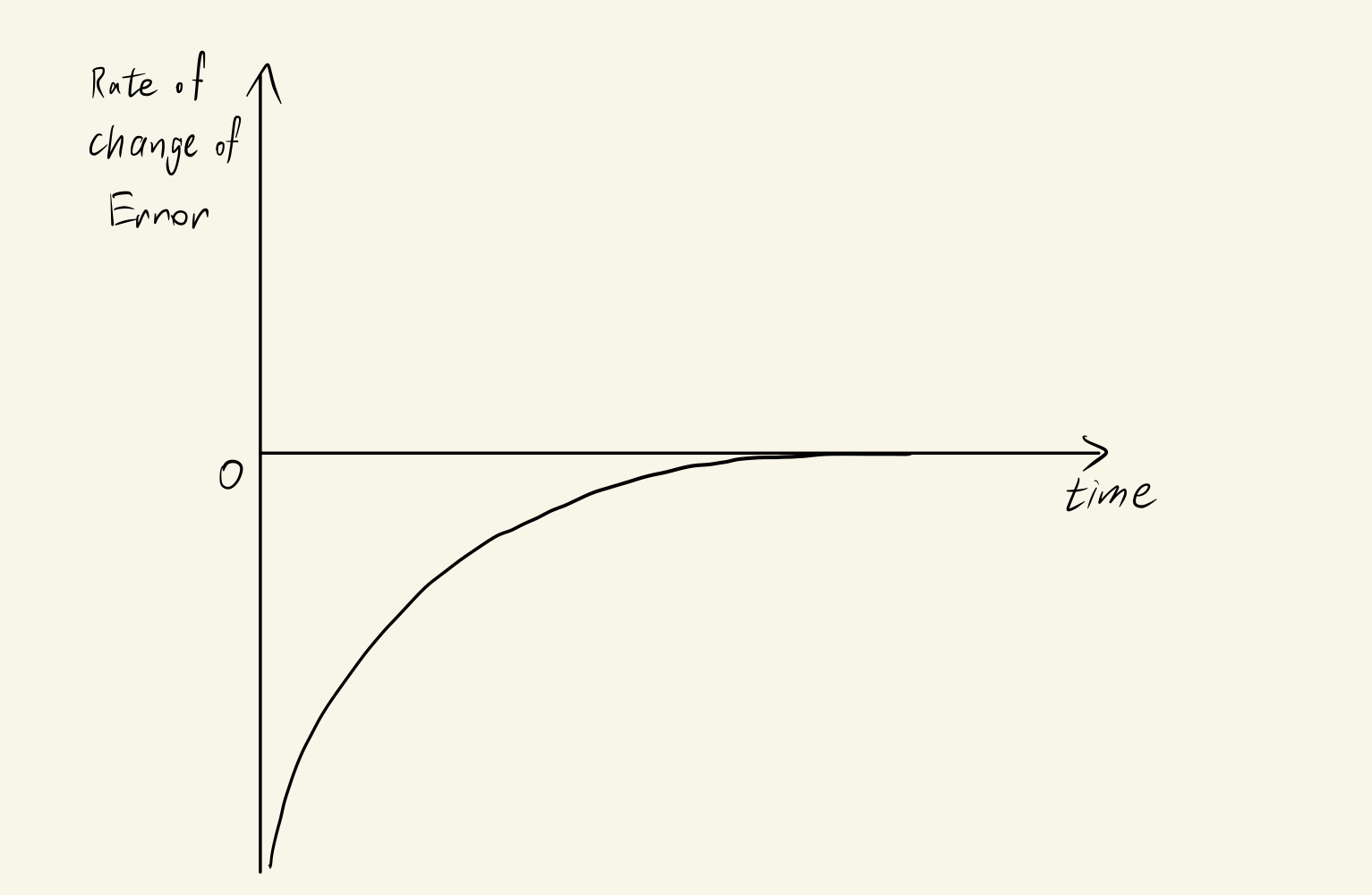
The negative value of the Derivative would be added to our controller output, as a result, lowering the speed of raising of Oil (or lowering the propeller speed of Oil's Take-Copter). So what Derivative Controller do, is to determine whether Oil is approaching the goal or not, and slow down Oil's rising to prevent Oil from overshooting.
To use the Derivative Controller, we have to define a constant "kd". It is used to multiply by the rate of change of the current Error.
D=kd∗dtde(t) kd: constant determined by yourself
How to Determine the optimal value for kd?
Generally, kd is much smaller than kp but larger than ki. But there are also some cases in which the kd is higher than kp.
PID Controller
After learning each separate controller, we can integrate them together to form our complete PID Controller. Basically, we just have to add the calculated "P", "I" and "D" to the Input of the Plant to complete our PID Controller.
Steps to tune the PID Controller
How can we find out the best value of "kp", "ki" and "kd" such that we can tune the best PID Controller?
Implement the complete formula of PID Controller:
Set "ki" and "kd" to zero, i.e. ki = 0 and kd = 0
Start tuning "kp" with 1, i.e. kp = 1. If the Output of the Plant takes a very long time to reach the Setpoint without overshooting, it means you have to use a larger "kp". However, if it overshoots, you can determine if the overshooting is controllable (which means will it keep overshooting and can never get back to the Setpoint). If it is controllable, you can keep using the "kp" and move on to tune the "kd"
After you find a "kp" that can let the Output overshoot but will eventually stay steady at the Setpoint, you can start tuning the "kd" with half of your "kp" (i.e. if your "kp" is 1, then you can start with kd = 0.5). Tune the kd until the Output of the Plant can reach the Setpoint without overshooting. If you keep increasing (or decreasing) the "kd" but the Output seems to have a larger extent of overshooting, you can try to decrease (or increase) your "kd".
After you have finished tuning the "kp" and "kd" for your PID Controller, you have to determine whether your Plant needs an Integrational Controller, which means you have to determine whether the Output of your Plant will be affected by any Steady State Error or constant Error. If yes, then you have to tune the constant "ki", starting with a very small value, until the output of the Plant can reach the Setpoint without undershooting eventually.
The values of kp, ki and kd are related to each other, so you may need to go back and change the value of kp again if it cannot reach the target quickly.
It seems to be hard to tune the PID Controller, but it all is about experiences. The more experience you get in tuning the PID Controller, the faster you can finish tuning it (also the faster you can find the optimal value for "kp", "ki", and "kd").
Try It Yourself
Congratulations, you have finished learning the PID Controller theoretically. All you have to do now is to try tuning it by yourself. Here is a nice website for you to train your "PID Tuning Skills".
You are required to use JavaScript to write programs such that the Block can reach its destination as soon as possible.
block.x: The current position of the Block
block.dx: The current speed of the Block
Block.T: The current time of the simulation. Destination of the Block: 0.00
As the destination of the block is 0, the value of the block.x would be the error.

If you have no clue about writing programs with JavaScript, here are some tips:
var : To declare a variable (No need to care about the type of the variable (i.e. You do not have to care whether the declared variable is an integer, float or whatever))
return : To return the Input to the Block.
There are several different games provided on the above website. Feel free to explore by yourself and try each of them out using the PID Controlling System.
(By the way, it only takes 0.4s for the Block to go to its destination in Tutorial #1 and Tutorial #2 and it only takes 1.16s for the Block to go to its destination in Tutorial #3 for me (Of course I am not cheating! I really tune the PID Controlling System by myself!). You are very welcome to challenge me and tell me your best record.)
References
You can go and watch these YouTube videos to further understand PID Controller if you still do not understand what PID is after reading these notes:
If you want to watch some real examples of PID applications, this is a good video for you:
Last updated
